What is number system in computer? Explain with Examples

---

In computer science, a number system is a way of representing numerical values using a set of symbols or digits. The most commonly used number systems in computers are the decimal system, the binary system, and the hexadecimal system.

What is the base of number system in computer?

The base, or radix, of a number system in computer science refers to the number of digits or symbols used to represent numerical values. In other words, the base determines how many unique values can be represented with a single digit in the number system.

The most commonly used number systems in computer science are:

• Decimal system (base 10) - uses 10 digits (0-9)
• Binary system (base 2) - uses 2 digits (0 and 1)
• Octal system (base 8) - uses 8 digits (0-7)
• Hexadecimal system (base 16) - uses 16 digits (0-9 and A-F)

In general, a number system with a higher base can represent more unique values with a smaller number of digits. For example, the binary system (base 2) can only represent 2 unique values with a single digit (0 and 1), while the decimal system (base 10) can represent 10 unique values (0-9) with a single digit.

The hexadecimal system (base 16) can represent 16 unique values (0-9 and A-F) with a single digit.

What is the use of number system in computer?

Number systems are a fundamental part of how computers represent and manipulate data. Computers use binary (base-2) number system to represent data and perform calculations. Here are some specific uses of number systems in computers:

• Representing data:

Computers use the binary number system to represent all kinds of data, such as text, images, audio, and video. Each piece of data is converted into a series of 0s and 1s, which can be stored and processed by the computer.

• Arithmetic operations:

Computers use the binary number system to perform arithmetic operations, such as addition, subtraction, multiplication, and division. These operations are performed using circuits and logic gates that manipulate binary values.

• Memory addressing:

Memory in a computer is organized into a series of addressable locations. The number of locations is determined by the number of bits used to represent each memory address. For example, a 32-bit computer can address up to 4 GB of memory.

• Computer programming:

Computer programming involves working with numbers and mathematical operations. Programmers use number systems such as binary, decimal, and hexadecimal to represent and manipulate data in their programs.

Overall, the use of number systems is essential to the functioning of computers and computer-based technologies

Types of number system in computer:

There are several types of number systems used in computer science, including:

• Binary:

The binary number system uses two digits, 0 and 1, to represent all numbers. It is the foundation of all digital systems, including computers.

• Decimal:

The decimal number system uses ten digits, 0 through 9, to represent all numbers. It is the number system most commonly used by humans.

• Octal:

The octal number system uses eight digits, 0 through 7, to represent all numbers. It is commonly used in computer programming and digital electronics.

• Hexadecimal:

The hexadecimal number system uses 16 digits, 0 through 9 and A through F, to represent all numbers. It is often used in computer programming and digital electronics because it is more compact and easier to read than binary.

In computer science, binary is the most commonly used number system, as it is the foundation of all digital systems. However, decimal, octal, and hexadecimal are also used in various applications.

Number System	Base	Example
Binary Number System	2	01010101
Octal Number System	8	125 163 141
Hexadecimal Number System	16	a5e3c1d5c1
Decimal Number System	10	85 115 97 109 97

What is binary number system in computer?

The binary number system is a base-2 number system used in computers to represent all types of data, including numbers, text, images, and sound. It is called "binary" because it uses only two digits, 0 and 1, to represent any number.

In the binary system, each digit represents a power of 2, starting from the rightmost digit, which represents 2⁰ or 1, and increasing by a power of 2 for each subsequent digit.

For example, the binary number 1010 represents:

= (1 x 2³) + (0 x 2²) + (1 x 2¹) + (0 x 2⁰)

= 8 + 0 + 2 + 0

= 10 in decimal form.

Computers use the binary number system to represent data because electronic circuits can only distinguish between two states, such as high voltage and low voltage, which can be mapped to the binary digits 1 and 0.

This allows computers to perform operations on data using simple logic circuits, which are made up of a combination of switches, transistors, and other electronic components.

Application of Binary number system in computer:

The binary number system is fundamental to the operation of computers. Computers are built to manipulate binary values, and all digital data is represented using binary digits, or bits.

Here are some specific applications of the binary number system in computers:

• Storage of data:

All data in a computer, including text, images, and videos, are stored as a sequence of binary digits, either 0s or 1s.

• Arithmetic operations:

Arithmetic operations such as addition, subtraction, multiplication, and division are performed using binary numbers.

• Logic operations:

Logic operations, such as AND, OR, and NOT, are used to compare and manipulate binary values to make decisions or perform actions.

• Memory addressing:

In a computer's memory, each byte of information is assigned a unique binary number, which is used to locate and retrieve data from the memory.

• Communication protocols:

Communication between different devices and systems is often accomplished through binary-based communication protocols, such as Ethernet and USB.

• Machine instructions:

All instructions executed by a computer's processor are represented in binary code. These instructions tell the computer what operations to perform on the data.

Binary number system example:

In this section, we’ll cover how can we convert the other number systems into binary.

Example 1:

Convert the following numbers into Binary

1. (25)₁₀
2. (71)₈

Solution:

• (25)₁₀

 

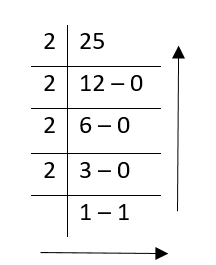
(25)₁₀ = (11000)₂

• (71)₈

               

 

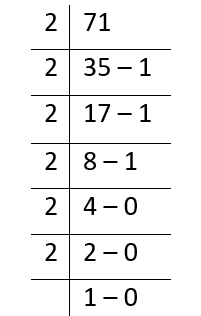
(71)₈ = (1000111)₂

What is decimal number system in computer?

The decimal number system is a base-10 number system used in everyday life, in which each digit can take one of ten possible values (0, 1, 2, 3, 4, 5, 6, 7, 8, or 9). In computer science, decimal numbers are typically represented using the binary number system, which is a base-2 system.

To represent decimal numbers in a computer, they are typically converted to binary using an algorithm. In binary representation, each digit represents a power of 2.

For example:

In the decimal number 123

The "1" represents 100 (or 1 * 10²)

The "2" represents 20 (or 2 * 10¹)

The "3" represents 3 (or 3 * 10⁰).

To convert this to binary, each of these values would be converted to binary using the base-2 system and then added together.

For example:

100 in binary is 1100100

20 in binary is 10100

3 in binary is 11

So, the binary representation of the decimal number 123 would be 1111011.

Most modern computers use binary floating-point representation to store decimal numbers. This allows for more precise calculations and a wider range of values to be represented than using a purely decimal system.

Application of decimal number system in computer

Decimal numbers are very helpful and play a vital role in our daily life calculations. Some basic applications of decimal numbers are as follows:

• The decimal number system is used by humans to represent and manipulate numbers in their daily life. However, computers use a binary number system, which is a base-2 number system.

The binary number system only has two digits, 0 and 1, which is more suited for electronic circuits to represent and process data.

• Although computers use a binary number system, decimal numbers are still important in computer systems, especially when it comes to the input and output of data. For example, when you enter a number into a computer, you generally use the decimal system.

But the computer will convert that number into binary to process it. Similarly, when the computer provides output, it may convert the binary results back to decimal for human-readable display.

• Decimal numbers are also important in programming languages. Many programming languages, such as Java and Python, have built-in functions that allow you to convert binary numbers into decimal numbers and vice versa.
• Additionally, decimal numbers can be used to represent floating-point numbers, which are commonly used in scientific and financial calculations.

Decimal number system Example:

In this section, we’ll cover the conversions of octal and binary numbers into decimal number system.

Example 1:

Convert the following numbers into Decimal

• (11010)₂
• (46)₈

Solution:

• (11010)₂

Step 1: Separate the digits and multiply them with “2” raise to the power (descending sequence)

= 1 * 2⁴ + 1 * 2³ + 0 * 2² + 1 * 2¹ + 0 * 2⁰

= 1 * 16 + 1 * 8 + 0 + 1 * 2 + 0

= 16 + 8 + 2

= (26)₁₀

• (46)₈

Step 1: Separate the digits and multiply them with “8” raise to the power (descending sequence)

= 4 * 8¹ + 6 * 8⁰

 = 4 * 8 + 6 * 1

= (38)₁₀

What is octal number system in computer?

The octal number system is a base-8 number system commonly used in computer systems to represent and store data. The octal number system uses the digits 0 to 7 to represent numbers. Each digit in an octal number represents a power of 8, starting from the rightmost digit.

For example:

The octal number 137 can be converted to decimal as follows:

= 1 * 8² + 3 * 8¹ + 7 * 8⁰

= 64 + 24 + 7

= 95 (decimal)

Octal numbers are often used in computer programming to represent bit patterns, where each octal digit represents three bits. This is because 2^3 = 8, so three bits can be combined to represent any of the eight possible values in the octal system.

Application of Octal number system in computer:

Octal number system is a positional numeral system that uses base-8 as its radix. In computer systems, octal numbers are commonly used to represent binary numbers in a more compact and readable format. Here are some common applications of octal numbers in computer systems:

• File permissions:

In Unix and Unix-like operating systems, file permissions are represented as three sets of three bits. Each set corresponds to the owner, group, and others. The three bits in each set represent read, write, and execute permissions.

These nine bits can be represented as a single octal digit, where each bit represents a power of 2. For example, the octal digit 644 represents read/write for the owner, read for the group, and read for others.

• Assembly language:

In assembly language programming, octal numbers can be used to represent machine code instructions. For example, the instruction to load the contents of a memory address into a register might be represented as 1256, where 1 is the opcode for the load instruction, and 256 is the memory address.

• PDP-8 computer:

The PDP-8 was a popular computer system in the 1960s and 1970s. It used an octal number system to represent instructions and data. Each instruction was represented as a 12-bit octal number, and memory addresses were also represented in octal.

• Debugging:

In some debugging tools, memory addresses and data values are represented in octal. This makes it easier to read and interpret the values, as each octal digit corresponds to three binary bits.

Overall, while the use of octal numbers has declined in modern computer systems, it remains an important part of computer history and some legacy systems still use it.

Octal number system example:

In this section, we’ll the steps to convert binary and decimal numbers into an octal number.

Example 1: Convert the following terms into octal number terms

• 108 with base 10
• 100101 with base 2

Solution:

• 108 with base 10

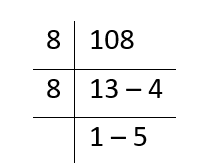
(108)₁₀ = (154)₈

• 100101 with base 2

Step 1: First convert this number into decimal number system

= 1 * 2⁵ + 0 * 2⁴ + 0 * 2³ + 1 * 2² + 0 * 2¹ + 1 * 2⁰

= 32 + 0 + 0 + 4 + 1

= 37

Step 2: Now convert it into octal

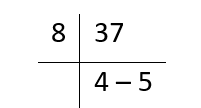
So, (100101)₂ = (45)₈

What is hexadecimal number system in computer?

In computing, the hexadecimal number system is a base-16 numbering system that uses 16 distinct symbols to represent numbers. The symbols used are 0-9 and A-F, where A represents the decimal value 10, B represents 11, and so on up to F, which represents 15.

The use of hexadecimal in computing is because it provides a convenient way to represent binary data, which is the native language of computers. Each digit in a hexadecimal number represents four bits (also called a "nibble") in binary.

For example:

The hexadecimal number "2A" represents the binary value "00101010", where the first four bits are represented by the "2" and the last four bits are represented by the "A".

Hexadecimal numbers are commonly used in computer programming, particularly in low-level programming, where it is important to manipulate individual bits or bytes of data. Hexadecimal is also used in computer networking, where it is used to represent IP addresses and other networking protocols.

Applications of hexadecimal number system in computer:

Hexadecimal (or "hex" for short) is a base-16 number system that is commonly used in computer science and digital electronics. Hexadecimal is used because it allows a compact representation of binary data, which is the basic language of computers. Here are some common applications of hexadecimal in computing:

• Memory addresses:

In computer memory, each byte of data is given a unique address. These addresses are typically represented in hexadecimal form since it is more compact than using a decimal or binary representation.

• Color codes:

Hexadecimal is often used to represent colors in web design and graphics. Each color is represented by a six-digit hexadecimal number, with two digits each for red, green, and blue. This system allows for millions of possible colors to be represented using just six characters.

• ASCII and Unicode encoding:

The American Standard Code for Information Interchange (ASCII) and Unicode are two-character encoding systems used to represent text in computers. Both use hexadecimal to represent characters, with each character assigned a unique hexadecimal code.

• File formats:

Many file formats use hexadecimal to represent data. For example, the Portable Document Format (PDF) uses hexadecimal to represent characters, images, and other data within the file.

• Network addresses:

In computer networking, IP addresses and other network addresses are often represented in hexadecimal form. This allows for easy manipulation and calculation of addresses.

Hexadecimal number system example:

In this section, the steps of converting a binary, decimal, and octal number into hexadecimal numbers are explained briefly.

Example 1: Convert the following terms into Hexadecimal number system

• (481)₁₀
• (110110)₂
• (61)₈

Solution:

• (481)₁₀

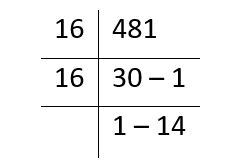
In Hexadecimal number system, “14” can be written as “E”

So, (481)₁₀ = (1E1)₁₆

• (110110)₂

Step 1: Convert it into decimal number first.

= 1 * 2⁵ + 1 * 2⁴ + 0 * 2³ + 1 * 2² + 1 * 2¹ + 0 * 2⁰

= 32 + 16 + 0 + 4 + 2 + 0

= 54

Step 2: Now convert it into hexadecimal number.

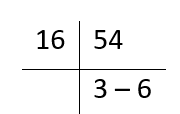
So (110110)₂ = 36

• (61)₈

Step 1: Conversion into decimal:

= 6 * 8¹ + 1 * 8⁰

= 48 + 1

= 49

Step 2: Conversion into Hexadecimal

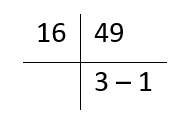
So, (61)₈ = (31)₁₆

_{Basic Number System Value Relationship}

Value	HEXADECIMAL	DECIMAL	OCTAL	BINARY
0	0	0	0	0000
1	1	1	1	0001
2	2	2	2	0010
3	3	3	3	0011
4	4	4	4	0100
5	5	5	5	0101
6	6	6	6	0110
7	7	7	7	0111
8	8	8	10	1000
9	9	9	11	1001
A	A	`10	12	1010
B	B	11	13	1011
C	C	12	14	1100
D	D	13	15	1101

Frequently Asked Questions

Here are some frequently asked questions of number system in computer.

Q: What is the importance of number system in computer?

Number system plays an important role in computer in the form of binary numbers because computers are digital and these devices are operated on binary digits. Different kinds of number system are used in computer to process and analyze information.

Q: Why do computers use binary numbers?

All the computers are based on electronic circuits in which only two states are available such as on and off. In this regards, binary numbers play a vital role as they contain 0 and 1 integers that are used to represent off and on respectively. Binary numbers are essential in computers for storing and processing information.

Q: Why do programmers use hexadecimal numbers?

Hexadecimal provides a compact way for the representation of binary numbers (0, 1). Programmers use hexadecimal numbers for making work easier and visualize large numbers as these kind of numbers are used to represent 4 bits of binary data.

Q: What is the relationship between number systems and computer memory?

Computer memory (RAM, ROM, or Cache) is organized into binary bits or digits that can store 1 or 0. Binary number is the most common way to store memory among all the number systems.

Q: What is the role of number systems in computer programming?

For representing and manipulating data in computers programming, number systems are used comprehensively. For working effectively while programming, a programmer must be familiar with various kinds of number systems and how to convert them.