Binary Translator
Prepostseo's Binary Translator Convert Binary code to Text (English or ASCII) and vice versa. Just paste your binary number in the input box and our tool will convert it automatically.
Table of Contents
Binary Translator
Binary translator is a tool to translate binary code into text for reading or printing purposes. You can translate binary to English by using two methods; ASCII and Unicode.
How to use Binary to Text converter?
Our binary to text translator has a very simple and user-friendly interface. Follow the below steps to convert the binary number into different formats
- Select the input type from the drop-down menu
- You can upload a .txt file or, Paste your relevant code in the Input box.
- Select the output type
- Hit the Convert Button
- You can “copy or download” your result
- You can swap the input boxes by clicking on the “Swap” button
- Click on the “reset” button to enter new values
Key Features of Binary Translator:
This binary translator is a unique tool that gives you some outstanding features:
- You can upload a file or a document from local storage.
- You can do multiple conversions like binary to hexadecimal, binary to octal, binary to decimal, and vice versa.
- This binary to text converter is 100% accurate.
- It does the conversions instantly without pressing any button.
- You can copy or download the report.
Applications of Binary Code Translator:
- The most common application for this number system can be seen in computer technology. After all, the basis for all computer language and programming is a two-digit number system used in digital encoding.
- This is what makes up the digital encoding process by taking data and then depicting it with restricted bits of information. The restricted information consists of the 0s and 1s of the binary system. The images on your computer screen are an example of this. For encoding these images, a binary line is used for each pixel.
- If a screen uses a sixteen-bit code, instructions will be given to each pixel on which color to display based on which bits are 0s and which are 1s. The result of this is more than 65,000 colors represented by 2 ^ 16. In addition to this, you will find the application of the binary number system in a mathematics branch known as Boolean algebra.
- The values of logic and truth concern this field of mathematics. In this application, statements are assigned a 0 or 1 based on whether they are true or false. You may want to try a binary to text converter, Decimal to Binary, or Binary to decimal Converter, if you're looking for a tool that helps in this application.
What is Binary Numeral System?
The binary decoder system is based on the number 2 (radix). It consists of only two numbers as a base-2 numeral system: 0 and 1.
While it was applied for various purposes in ancient Egypt, China, and India. The binary system has become the modern world's language of electronics and computers.
This is the most efficient system for detecting the OFF (0) and ON (1) state of an electrical signal.The Binary numeral system uses the combination of 0’s and 1’s to represent a number between 0 to 9. This combination is easily readable by the computer, each digit of that combination is known as bit.
Difference between Bit and Byte:
1 bit. Bit and Byte are two significant units in the binary number system, “one-bit” represents the single digit of a binary number whereas “one-byte” is equal to “8-bits”
Crazy fact:
It's easier to read a binary number than it looks: this is a positional system; therefore, every digit in a binary number is raised to the powers of 2, starting with 20 from the right. Each binary digit in the binary code converter refers to.
What’s ASCII?
ASCII is an international standard used for encoding characters in electronic communication, abbreviated from the American Standard Code for Information Interchange. In computers, telecommunications equipment, and other devices, ASCII codes represent text. While many additional characters are supported, most modern character encoding schemes are based on ASCII.
ASCII is the traditional name for the encoding system; the Internet Assigned Numbers Authority (IANA) prefers the updated U.S.-ASCII name, which clarifies that this system was developed in the U.S. and based on the predominantly used typographic symbols.
ASCII is one of the highlights of the IEEE.
Binary to ASCII
Originally based on the English alphabet, ASCII encodes 128 specified seven-bit integer characters. Ninety-five encoded characters are printable, including digits 0 to 9, lower case letters a to z, upper case letters A to Z, and symbols for punctuation. Furthermore, 33 non-printing control codes originating with Teletype machines were included in the original ASCII specification; most of these are now obsolete, although some are still commonly used, such as carriage return, line feed and tab codes.
For example, binary 1101001= hexadecimal 69 (i is the ninth letter) = decimal 105 would represent lowercase I in the ASCII encoding.
Uses of ASCII
As mentioned above, using ASCII, you can translate computer text into human text. Simply put, it’s a binary to English translator.
All computers receive message in binary, 0 and 1 series. However, just as English and Spanish can use the same alphabet but for many similar things, they have completely different words, computers also have their own language version. ASCII is used as a method that allows all computers to share documents and files in the same language.
ASCII is important because computers were given a common language by the development.
In 1963, ASCII was first used commercially as a seven-bit teleprinter code for the TWX (Teletype Writer eXchange) network of American Telephone & Telegraph. Initially, TWX used the previous five-bit ITA2, which the competing Telex teleprinter system also used. Bob Bemer introduced features like the sequence of escape. His British colleague, Hugh McGregor Ross, helped popularize this work–"so much so that the code to become ASCII was first called the Bemer–Ross Code in Europe," according to Bemer. Because of his extensive ASCII work, Bemer was called "ASCII's father."
Until December 2007, when UTF-8 encoding surpassed it, ASCII was the most common character encoding on the World Wide Web; UTF-8 is backward compatible with ASCII.
UTF-8 (Unicode)
UTF-8 is a character encoding that can be as compact as ASCII, but can also contain any unicode characters (with some file size increase).
UTF is Unicode Transformation Format. The' 8' means representing a character using 8-bit blocks. The number of blocks that a character needs to represent varies from 1 to 4.
One of UTF-8's really nice features is that it is compatible with nul-terminated strings. When encoded, no character will have a byte nul (0).
Unicode and the Universal Character Set (UCS) of ISO / IEC 10646 have a much wider range of characters and their various encoding forms have started to quickly replace ISO / IEC 8859 and ASCII in many situations. While ASCII is limited to 128 characters, Unicode and UCS support more characters through the separation of unique identification concepts (using natural numbers called code points) and encoding (up to UTF-8, UTF-16, and UTF-32-bit binary formats).
Difference between ASCII & UTF-8
| ASCII | UTF - 8 |
| It is a character encoding standard | It provides a unique way to represent almost all characters, that are generally spoken in the world |
| ASCII represent 128 characters | It represents more than 140000 characters |
| ASCII only supports English characters | UTF-8 supports special characters and emojis. |
| ASCII is the subset of UTF-8 | UTF-8 is the superset of ASCII |
| ASCII represents a smaller range | UTF-8 represents a wide range of characters |
Key Advantages of the Binary Number System:
The binary number system is useful for a number of things. For instance, a computer flips switches to add numbers. You can stimulate computer adding by adding binary numbers to the system. There are now two main reasons for using this computer number system. Firstly, it can provide a reliable safety range. Secondly and most importantly, it helps to minimize the necessary circuitry. This reduces the space needed, the energy consumed, and the expenditure.
Fun Fact
You can encode or translate binary messages written in binary numerals. For example,
(01101001)(01101100011011110111011001100101)(011110010110111101110101) is a decoded message. When you will copy paste these numbers in our binary translator, you will get the following English text:
I Love You
That means
(01101001)(01101100011011110111011001100101)(011110010110111101110101) = I Love You
Some Common Values Table of Binary Code Translation
| Binary | Hexadecimal | ASCII |
|---|---|---|
| 00000000 | 00 | NUL |
| 00000001 | 01 | SOH |
| 00000010 | 02 | STX |
| 00000011 | 03 | ETX |
| 00000100 | 04 | EOT |
| 00000101 | 05 | ENQ |
| 00000110 | 06 | ACK |
| 00000111 | 07 | BEL |
| 00001000 | 08 | BS |
| 00001001 | 09 | HT |
| 00001010 | 0A | LF |
| 00001011 | 0B | VT |
| 00001100 | 0C | FF |
| 00001101 | 0D | CR |
| 00001110 | 0E | SO |
| 00001111 | 0F | SI |
| 00010000 | 10 | DLE |
| 00010001 | 11 | DC1 |
| 00010010 | 12 | DC2 |
| 00010011 | 13 | DC3 |
| 00010100 | 14 | DC4 |
| 00010101 | 15 | NAK |
| 00010110 | 16 | SYN |
| 00010111 | 17 | ETB |
| 00011000 | 18 | CAN |
| 00011001 | 19 | EM |
| 00011010 | 1A | SUB |
| 00011011 | 1B | ESC |
| 00011100 | 1C | FS |
| 00011101 | 1D | GS |
| 00011110 | 1E | RS |
| 00011111 | 1F | US |
| 00100000 | 20 | Space |
| 00100001 | 21 | ! |
| 00100010 | 22 | " |
| 00100011 | 23 | # |
| 00100100 | 24 | $ |
| 00100101 | 25 | % |
| 00100110 | 26 | & |
| 00100111 | 27 | ' |
| 00101000 | 28 | ( |
| 00101001 | 29 | ) |
| 00101010 | 2A | * |
| 00101011 | 2B | + |
| 00101100 | 2C | , |
| 00101101 | 2D | - |
| 00101110 | 2E | . |
| 00101111 | 2F | / |
| 00110000 | 30 | 0 |
| 00110001 | 31 | 1 |
| 00110010 | 32 | 2 |
| 00110011 | 33 | 3 |
| 00110100 | 34 | 4 |
| 00110101 | 35 | 5 |
| 00110110 | 36 | 6 |
| 00110111 | 37 | 7 |
| 00111000 | 38 | 8 |
| 00111001 | 39 | 9 |
| 00111010 | 3A | : |
| 00111011 | 3B | ; |
| 00111100 | 3C | < |
| 00111101 | 3D | = |
| 00111110 | 3E | > |
| 00111111 | 3F | ? |
| 01000000 | 40 | @ |
| 01000001 | 41 | A |
| 01000010 | 42 | B |
| 01000011 | 43 | C |
| 01000100 | 44 | D |
| 01000101 | 45 | E |
| 01000110 | 46 | F |
| 01000111 | 47 | G |
| 01001000 | 48 | H |
| 01001001 | 49 | I |
| 01001010 | 4A | J |
| 01001011 | 4B | K |
| 01001100 | 4C | L |
| 01001101 | 4D | M |
| 01001110 | 4E | N |
| 01001111 | 4F | O |
| 01010000 | 50 | P |
| 01010001 | 51 | Q |
| 01010010 | 52 | R |
| 01010011 | 53 | S |
| 01010100 | 54 | T |
| 01010101 | 55 | U |
| 01010110 | 56 | V |
| 01010111 | 57 | W |
| 01011000 | 58 | X |
| 01011001 | 59 | Y |
| 01011010 | 5A | Z |
| 01011011 | 5B | [ |
| 01011100 | 5C | \ |
| 01011101 | 5D | ] |
| 01011110 | 5E | ^ |
| 01011111 | 5F | _ |
| 01100000 | 60 | ` |
| 01100001 | 61 | a |
| 01100010 | 62 | b |
| 01100011 | 63 | c |
| 01100100 | 64 | d |
| 01100101 | 65 | e |
| 01100110 | 66 | f |
| 01100111 | 67 | g |
| 01101000 | 68 | h |
| 01101001 | 69 | i |
| 01101010 | 6A | j |
| 01101011 | 6B | k |
| 01101100 | 6C | l |
| 01101101 | 6D | m |
| 01101110 | 6E | n |
| 01101111 | 6F | o |
| 01110000 | 70 | p |
| 01110001 | 71 | q |
| 01110010 | 72 | r |
| 01110011 | 73 | s |
| 01110100 | 74 | t |
| 01110101 | 75 | u |
| 01110110 | 76 | v |
| 01110111 | 77 | w |
| 01111000 | 78 | x |
| 01111001 | 79 | y |
| 01111010 | 7A | z |
| 01111011 | 7B | { |
| 01111100 | 7C | | |
| 01111101 | 7D | } |
| 01111110 | 7E | ~ |
| 01111111 | 7F | DEL |
Frequently Asked Questions
Is 00000000 a valid byte?
Yes, 00000000 (or 0x00 in hexadecimal notation) is a valid byte value. It represents the numerical value 0 in binary representation and can be used to represent any data stored in a byte.
How to read binary?
Reading binary involves understanding the basic concepts of the binary number system, which uses only two digits, 0 and 1. Each digit, or "bit", represents a power of 2. The rightmost digit represents 2^0 (or 1), the next digit to the left represents 2^1 (or 2), the next represents 2^2 (or 4), and so on.
Who invented binary?
The concept of binary notation has been attributed to several ancient cultures, such as the ancient Egyptians and the Chinese. The use of binary as a way to represent numbers in electronic systems was the first invention of Gottfried Wilhelm Leibniz, who began using the binary system in the late 17th century.
Can binary start with 0?
Yes, a binary number can start with the digit 0.
E-g: the binary number 0001 is equivalent to the decimal value 1, and the binary number 0000 is equivalent to the decimal value 0.
What is the shortest binary?
The shortest binary number is "0" (zero), which is a single digit and represents the decimal value 0.
The shortest possible binary number in a byte is "00000000", which also represents the decimal value 0.
Is 400 a binary number?
No, 400 is not a binary number. Binary numbers only use the digits 0 and 1.
You can convert it to binary using the following method:
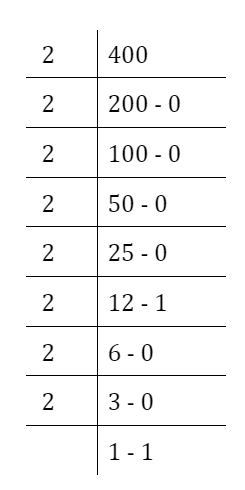
400 in decimal = 110010000 in binary.
Is 200 a binary number?
No, 200 is not a binary number. In binary code of 200 is 11001000.
What does 01101000 01100101 01101100 01101100 01101111 mean in binary?
Using our binary converter 01101000 01100101 01101100 01101100 01101111 means “hello”.
What does 0100100001101001 mean in binary?
The binary code 0100100001101001 means Hi.
Here are some more examples
1010101010 in binary means ª. It's “a” alphabet in uppercase.
666 written in binary as 1010011010.
To say love in binary will be 01101100 01101111 01110110 01100101.
36 in binary is 100100
170 in binary is 10101010
162 in binary is 10100010
192 in binary is 10111110
.45 in binary is 0.01110011001100110011
10101010 in decimal is 170.
0.75 in binary code is 0.11
